[Python][Scikit-learn] 多次元尺度構成法(MDS)で都内公園の時間地図を作成する

はじめに

都市間の距離の表や、個体間の類似度表から最適な二次元、三次元上の配置を推定し、類似した（距離が近い）ものを近くに、類似していない（距離が遠い）ものを遠くに配置する手法を多次元尺度構成法（Multidimensional Scaling）といいます。本記事ではこのMDSを用いて、都内23区内にある主要な10公園（面積の広さトップ10)を対象に公園間の移動時間から時間地図（所要時間を地図上の距離として表したもの）を作成してみました。

多次元尺度構成法（MDS）のしくみ

多次元尺度構成法の手法にはいくつかあり、下記のような分類があります。

• 計量MDS : 温度や身長、長さといった比例尺度や間隔尺度等の定量的数値データを対象に個体の類似度を計算し、最適な配置を算出します。
• 非計量MDS : 心理学、アンケート等で用いられる評価データのような定性的データ（順序が意味をもつ順序尺度に限る）も含めて類似度を計算し、最適な配置を算出します。

今回用いた手法は前者の計量MDSになります。そちらの仕組みを見ていきます。

まず計量MDSは次のような式で与えられるストレスという量を最小化するような配置の組み合わせ \( \boldsymbol{x}_1, \dots, \boldsymbol{x}_N \) をなんらかのアルゴリズムを用いて算出します。

[latex] \text{Stress}_D ( \boldsymbol{x}_1, \dots, \boldsymbol{x}_N) = \sqrt{ \sum_{i \neq j = 1, \dots, N} (d_{ij} - || \boldsymbol{x}_i - \boldsymbol{x}_j || )^2} [/latex]

この時 \( d_{ij} \) は与えられた個体間の類似度を表す行列 \( D \) の要素です。

このような量を最小化するためのアルゴリズムとして、Scikit-learnで用いられているのがSMACOF(Scaling by MAjorizing a COmplicated Function)ですが、その仕組みについては

Jan de Leeuw, Patrick Mair Multidimensional Scaling Using Majorization: SMACOF in R (2009)

を参照してみてください。Rのライブラリの解説ですが、数学的な背景とともにどのようなロジックで解に収束するかが記載されています。

データ・セット

今回対象としたデータ・セットは都内23区内にある公園のうち、面積が広いものを上から順に10個選び、その公園間の時間的な移動距離を概算の分単位で出した次のようなCSVデータになります。

park_time.csv

minamoto,0,70,60,90,70,60,80,100,110,80
kasairinkai,70,0,60,80,50,40,20,70,80,60
toneri,60,60,0,70,50,40,70,80,90,90
hikarigaoka,90,80,70,0,50,60,70,70,80,100
yoyogi,70,50,50,50,0,40,50,40,40,60
ueno,60,40,40,60,40,0,40,70,80,60
yumenoshima,80,20,70,70,50,40,0,70,80,60
komazawa,100,70,80,70,40,70,70,0,40,90
kinuta,110,80,90,80,40,80,80,40,0,100
shinozaki,80,60,90,100,60,60,60,90,100,0

こちらのデータを jupyter notebook と同一のディレクトリに入れてください。

再現のための手続き

いつもの様に、ソースコードはGithub上に上がっています。Scikit-learnのMDSを用いる部分とグラフ描画部分を中心に見ていきます。

動作環境

• anaconda-4.0.0

In [1]:

import numpy as np
from sklearn import manifold
import matplotlib.pyplot as plt
%matplotlib inline

In [2]:

datum = np.loadtxt("park_time.csv",delimiter=",",usecols=range(1,11))

CSVデータを読み込みます。一列目は公園を表すラベルのため、除外します。

In [4]:

mds = manifold.MDS(n_components=2, dissimilarity="precomputed", random_state=6)

Scikit-learnのMDSクラスを作成します。クラス作成時に渡している引数の意味は左から順に次の通りです。

• n_components : MDSを用いてマッピングする先の次元数（多くは2か3を指定）
• dissimilarity : 類似していない度合いの指定を行います。"precomputed" と "euclidean" の文字列のどちらかを指定し、前者はすでに個体間の類似度の行列に当てはまるデータがあるとき、後者は個体ごとに特徴ベクトルがあるデータに対して距離を計算し、類似度の行列の算出を行なってくれます。
• random_state : このコードによる配置の再現のために乱数シードを与えます。

In [5]:

pos = mds.fit_transform(datum)

SMACOFのアルゴリズムを実行し、与えられた類似度の行列に当てはまる最適な配置を算出します。

In [7]:

labels = np.genfromtxt("park_time.csv",delimiter=",",usecols=0,dtype=str)

CSVの一列目から公園を表すラベルの配列を取得します。

In [9]:

plt.scatter(pos[:, 0], pos[:, 1], marker = 'o')

for label, x, y in zip(labels, pos[:, 0], pos[:, 1]):
    plt.annotate(
        label,
        xy = (x, y), xytext = (70, -20),
        textcoords = 'offset points', ha = 'right', va = 'bottom',
        bbox = dict(boxstyle = 'round,pad=0.5', fc = 'yellow', alpha = 0.5),
        arrowprops = dict(arrowstyle = '->', connectionstyle = 'arc3,rad=0')
    )

plt.show()

これらのコードで公園の配置を表す座標と、その座標を表す公園のラベルと矢印を表示します。

• l1 : MDSをもとに算出された配置を二次元上にplotします。
• l4 : 配置に公園を表すラベルをつけます。
• l6 : ラベルをつける対象の座標と、テキストの位置を指定します。l7のtextcoordsで 'offset points' が指定されているので、対象の座標からのテキストの相対位置を表します。ha va でテキストから見てどの位置から矢印が伸びるかを指定します。この例だと右下から矢印がのびます。
• l8 : テキストを覆うボックスの形式を指定します。
• l9 : 矢印の形式を指定します。

上記コードで得られる図は下記の通りです。

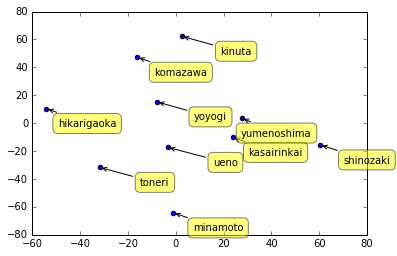
In [10]:

上の図だと現実の位置関係との比較を行いづらいため、少し座標変換を行い再び同じ位置関係の配置を表示してみます。

plt.figure()

angle = 120.
theta = (angle/180.) * np.pi

rotMatrix = np.array([[np.cos(theta), -np.sin(theta)], 
                         [np.sin(theta),  np.cos(theta)]])
revMatrix = np.array([[-1, 0], [0, 1]])

fixed_pos = rotMatrix.dot(revMatrix.dot(pos.T)).T
plt.scatter(fixed_pos[:, 0], fixed_pos[:, 1], marker = 'o')

for label, x, y in zip(labels, fixed_pos[:, 0], fixed_pos[:, 1]):
    plt.annotate(
        label,
        xy = (x, y), xytext = (60, 10),
        textcoords = 'offset points', ha = 'right', va = 'bottom',
        bbox = dict(boxstyle = 'round,pad=0.5', fc = 'yellow', alpha = 0.5),
        arrowprops = dict(arrowstyle = '->', connectionstyle = 'arc3,rad=0')
    )

plt.show()

• l3-6 : 120度の回転行列を作成します。
• l8 : x座標の反転変換を表す行列を作成します。
• l10 : 座標変換を行なった後の位置を行列を適用することで再度計算します。

上記コードで得られる図は以下のとおりです。

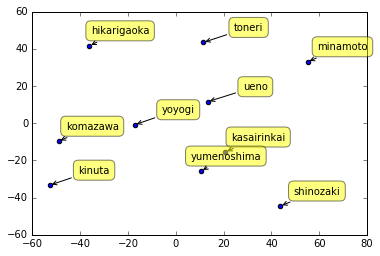
さて、現実の地図と比較してみましょう

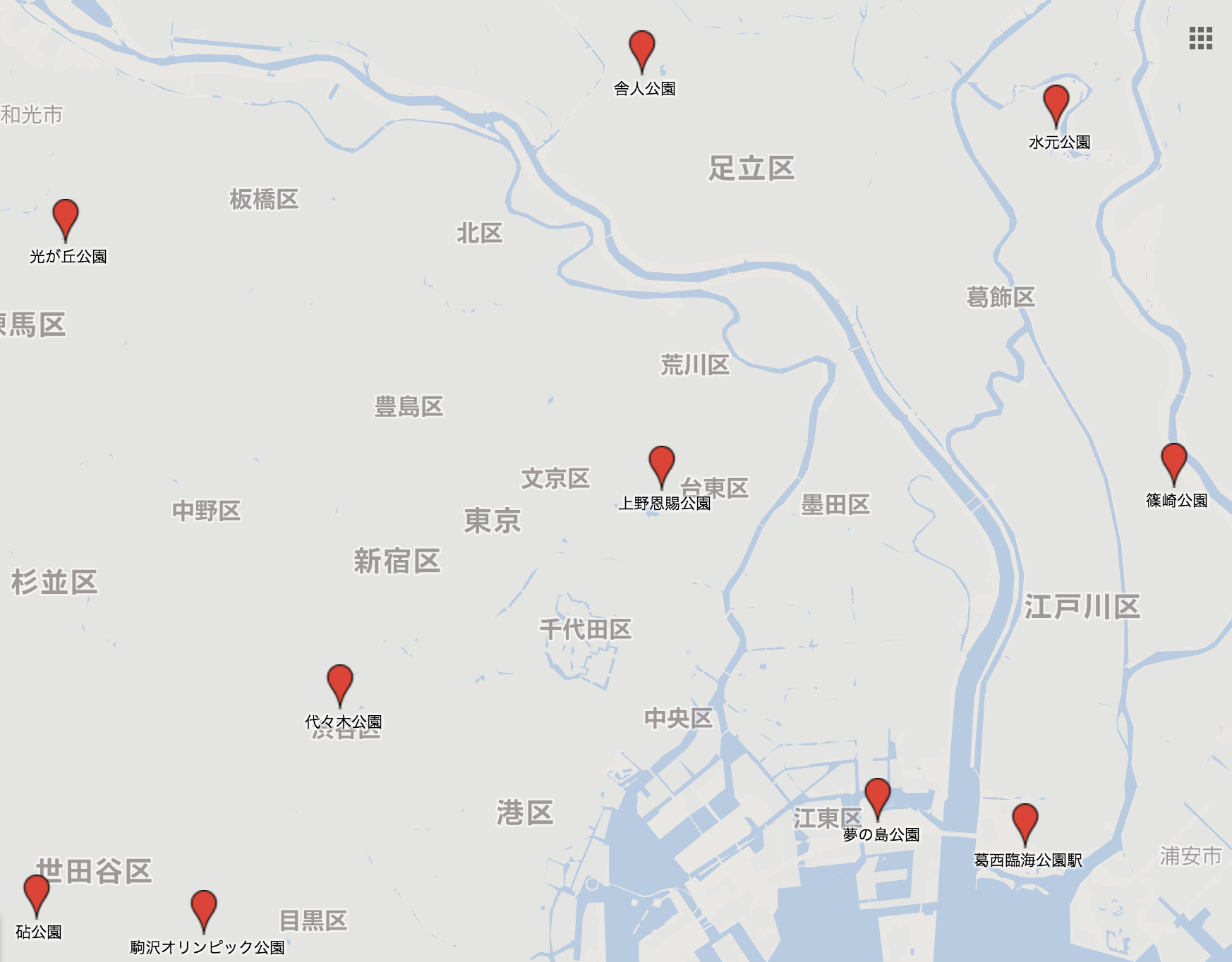
実世界の座標同士を比較した距離（座標距離）を類似度とするか、公園間の移動にかかる所要時間（時間距離）を類似度とするかで結構位置関係に違いが出てくることを予想していましたが、今回は在来線や徒歩のみということもあって、位置関係に余り違いが無いように見受けます。

ただ、千代田区を中心として放射状に広がる直線を想定したときに、同一の直線にある場合と異なる直線にある場合は乗り換えも含めて所要時間に大きな差が出ることが考えられるため、篠崎公園と水元公園は実際の座標距離に基づく位置関係と比べて時間距離がとられていることが伺えます。

多次元尺度構成法に関連する手法

多様体学習

今回はScikit-learnのmanifoldモジュールを用いましたが、manifoldは数学でいうところの多様体を表し、今回の手法もその一部と捉えられます。

この手法は一見高次元上にあるように見えるデータが、実は単純な低次元で表せる構造しか持っていないときに用いれます。これだけでもわかりにくいですが、例えばよく用いられる例としてはスイスロールがあります。

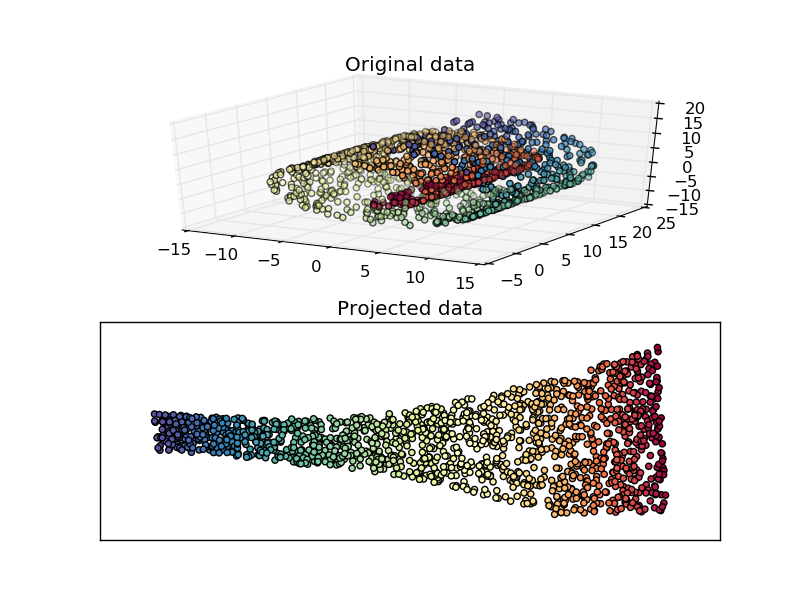(Swiss Roll reduction with LLE より)

この例ではスイスロールのクリームの部分にあたる箇所にデータが集中しており、このクリームの箇所を表す二次元平面上にデータを落とし込んでいます。

MDSも対象データを特徴ベクトルから考えた時、特徴ベクトル空間上から何らかの平面上にマッピングする処理とみなせるため、多様体学習の一部とみなせるということです。

まとめ

本手法は調査対象の個体間の距離や類似度が予め全てわかっている時に用いれる手法のため、欠損データがないケースにしか適用出来ません。ですが、データがそろっているとき、ひと目で全体の類似度が把握できるのが嬉しいです。7月下旬になって某スマホゲームがリリースされ、主要な公園をめぐるのに時間地図があるといいなと思ったのが本記事を執筆した動機になります。表で表されたデータも、図に落とし込んでみるとわかりやすいですね！

参考

• 金明哲 Rによるデータサイエンス - 森北出版 2007
• Multidimensional scaling - Wikipedia, the free encyclopedia (2016/8/1)
• Jan de Leeuw, Patrick Mair Multidimensional Scaling Using Majorization: SMACOF in R 2009